| Ciencias de Joseleg | Química | Química del equillibrio | Cinética química | (Ejercicios) (Introducción) (Generalidades) (Factores que afectan la velocidad de reacción) (Historia) (Velocidad de reacción) (Velocidades de aparición y desaparición) (Relación entre velocidades de aparición, desaparición y reacción) (Ley de velocidad de reacción) (Reacciones de primer orden) (Reacciones de segundo orden) (Reacciones de cero orden) (Vida media) (Energía de activación) (Mecanismo de reacción) (Catalizadores) (Referencias)
Las leyes
de velocidad que hemos examinado hasta ahora nos permiten calcular la velocidad
de una reacción a partir de la velocidad constante y las concentraciones de
reactivo. En esta sección, mostraremos que las leyes de velocidad también se
pueden convertir en ecuaciones que muestran la relación entre las
concentraciones de reactivos o productos y el tiempo. La matemática requerida
para lograr esta conversión implica cálculo y
ecuaciones diferenciales. No esperamos que pueda realizar las
operaciones de cálculo, pero debería poder usar las ecuaciones resultantes.
Aplicaremos esta conversión a tres de las leyes de tasas más simples: las de
primer orden general, las de segundo orden general y las de cero orden general.
Una
reacción de primer orden es aquella cuya velocidad depende de la concentración
de un solo reactivo elevado a la primera potencia. Si una reacción de los
productos tipo r → p es de primer orden, podemos
igualar dos ecuaciones para la velocidad promedio:
Esta forma
de ley de velocidad de reacción, que expresa cómo la tasa depende de la
concentración, se llama ley
de velocidad diferencial. Usando la operación de cálculo llamada integración,
esta relación puede transformarse en una ecuación conocida como la ley de tasa
integrada para una reacción de primer orden que relaciona la concentración
inicial de A, con su concentración en cualquier otro momento.
Formas integradas
🟦 DEMOSTRACIÓN. Deducir la función que permite calcular la concentración de una
sustancia cualquiera para cualquier momento de tiempo t partiendo de la
expresión de cambio instantáneo para una reacción de primer orden
La respuesta
puede expresarse en una forma logarítmica o en una forma euleriana:
🟦 DEMOSTRACIÓN. Modificar la ley de cinética de primer orden para poder utilizar
parámetros de gases como la presión en lugar de la concentración molar. Asuma
que la temperatura es constante.
La ventaja de la
forma euleriana radica en que al hacer análisis de regresión empleando Excel,
obtendremos precisamente una ecuación con una estructura que contiene el número
de Euler, lo cual será indicador que se trata de una ecuación de primer orden.
La forma linealizada es útil cuando no tienes un sistema de graficación
automático como Excel, pues la forma euleriana es una curva, mientras que la
forma logarítmica es una recta. Tenga en cuenta que el parámetro t toma
como referencia el momento inicial o cero (t0 = 0), por lo
que toda comparación de tiempo deberá tener en cuenta el tiempo absoluto desde
el inicio de la medición, lo que trae como consecuencia que todas las
concentraciones iniciales (c0) sean las concentraciones a (t0
= 0).
Para una
reacción de primer orden, la ecuación (9.2) y (9.4) puede despejarse para
hallar:
👉 la constante. Las ecuaciones 9.6 y 9.7 indican que las unidades de la
constante en una reacción de primer orden son unidades de frecuencia o se
tiempo inverso como s-1 o min-1.
👉 la concentración de un reactivo restante en cualquier momento después
de que la reacción haya comenzado,
👉 el intervalo de tiempo requerido para que una fracción dada de una
muestra reaccione, o
👉 el tiempo intervalo requerido para que una concentración de reactivo
caiga a cierto nivel.
Vida media
En cuanto
a la concentración de un reactivo restante en cualquier momento después de que
la reacción haya comenzado podemos tener una variación, normalmente esperamos
que nos pidan la concentración en valores absolutos a partir de la
concentración en valores absolutos. Sin embargo, podemos tener una solicitud de
calcular un valor relativo es decir un porcentaje de consumo. Normalmente el
porcentaje de consumo que más nos interesa es el 50% para calcular la vida
media de una sustancia, pero nos pueden pedir cualquier porcentaje del
reactivo.
🟦 DEMOSTRACIÓN. Demostrar la fórmula para calcular
el tiempo necesario para consumir cierto porcentaje de reactivo clave en una
reacción de cinética de primer orden.
✔️ Ejemplo. Hallar el tiempo requerido para
consumir el 50% del reactivo clave para cualquier valor de k.+
Tenga en cuenta que la vida media también puede estimarse gráficamente como el tiempo requerido para que cualquier concentración disminuya a la mitad.
Química de Chang10
✔️ Ejemplo 13.4.a. La conversión de ciclopropano a
propeno en fase gaseosa es una reacción de primer orden con una constante de velocidad
de 6.7 x 10-4 s-1 a 500°C. (a) Si la concentración
inicial de ciclopropano era de 0.25 M, ¿cuál es la concentración después de 8.8
min?
✔️ Ejemplo 13.4.b. La conversión de ciclopropano a propeno en fase gaseosa es una reacción
de primer orden con una constante de velocidad de 6.7 x 10-4 s-1
a 500°C. (b) ¿Cuánto tiempo (en minutos) tardará la concentración de
ciclopropano en disminuir de 0.25 M a 0.15 M?
✔️ Ejemplo 13.4.c. La conversión de ciclopropano a propeno en fase gaseosa es una reacción
de primer orden con una constante de velocidad de 6.7 x 10-4 s-1
a 500°C. (c) ¿Cuánto tiempo (en minutos) llevará convertir el 74 por ciento del
material de partida?
✔️ Práctica 13.4. La reacción 2A → B es de primer
orden en A con una constante de velocidad de 2.8 x 10-2 s-1
a 80°C. ¿Cuánto tiempo (en segundos) tardará A en disminuir de 0.88 M a 0.14 M?
✔️ Ejemplo 13.5. La velocidad de descomposición del azometano (C2H6N2)
se estudia controlando la presión parcial del reactivo en función del tiempo.
¿Son consistentes estos valores con la cinética de primer orden? Si es así, determine
la constante de velocidad
✔️ Práctica 13.5. El yoduro de etilo (C2H3I) se descompone a cierta
temperatura en fase gaseosa como sigue: C2H5I(g) → C2H4(g) + HI(g) A
partir de los siguientes datos, determine el orden de la reacción y la
constante de velocidad.
✔️ Ejemplo
13.6. La descomposición del etano (C2H6) en radicales
metilo es una reacción de primer orden con una constante de velocidad de 5.36 x
10-4 s-1 a 700 °C: C2H6(g) → 2CH3(g)
Calcule la vida media de la reacción en minutos.
✔️ Práctica 13.6. Calcular la vida media de la
descomposición de N2O5 si la constante de velocidad es
5.7 x 10-4 s-1.
✔️ Problema 13.19. El ciclobutano se descompone en etileno según la ecuación C4H8(g)
→ 2C2H4(g)
Determine el orden de la reacción y la constante de velocidad con base en las
siguientes presiones, que se registraron cuando la reacción se llevó a cabo a
430 °C en un recipiente de volumen constante.
✔️ Problema 13.20: La
siguiente reacción en fase gaseosa se estudió a 290 °C observando el cambio de
presión en función del tiempo en un recipiente de volumen constante: ClCO2CCl3(g)
→ 2COCl2(g) Determine
el orden de la reacción y la constante de velocidad con base en en los
siguientes datos a de presión.
Química la ciencia central 13
✔️ Muestra 14.7a. La descomposición de cierto insecticida en agua a 12 °C sigue una
cinética de primer orden con una tasa constante de 1.45 año-1. Una
cantidad de este insecticida se lava en un lago el 1 de junio, lo que lleva a
una concentración de 5.0x10-7 g/cm3. Suponga que la
temperatura del lago es constante (de modo que no haya efectos de variación de
temperatura en la velocidad, o que los cambios se concentración se anulan entre
si debido a su naturaleza cíclica). ¿Cuál es la concentración del insecticida
el 1 de junio del año siguiente?
✔️ Muestra 14.7b. La descomposición de cierto
insecticida en agua a 12 °C sigue una cinética de primer orden con una tasa
constante de 1.45 año-1. Una cantidad de este insecticida se lava en
un lago el 1 de junio, lo que lleva a una concentración de 5.0x10-7
g/cm3. Suponga que la temperatura del lago es constante (de modo que
no haya efectos de variación de temperatura en la velocidad, o que los cambios
se concentración se anulan entre si debido a su naturaleza cíclica). ¿Cuánto tiempo tomará para que la
concentración de insecticida disminuya a 3.0x10-7 g/cm3?
✔️ Práctica 14.7.1. A 25°C, la descomposición del
pentóxido de dinitrógeno en dióxido de nitrógeno y oxígeno sigue una cinética
de primer orden con una constante igual a 3.4 x 10-5 s-1.
Una muestra de N2O5 con una presión inicial de 760 torr se descompone a 25 °C
hasta que su presión parcial es de 650 torr. ¿Cuanto tiempo en segundos debe
haber pasado? (a) 5.3 x 10-6 (b) 2000 (c) 4600 (d) 34000 (e) 190000
✔️ Práctica 14.7.2. La descomposición del dimetil eter
(CH3)2O a 510 °C es un proceso de primer prden con una
constante de 6.8 x 10-4 s-1. Si la presión inicial de 135
torr, cual será la presión después de 1420 s.
✔️ Muestra 14.9. La reacción de C4H9Cl con agua es una reacción de
primer orden. (a) Estimar la vida media de esta reacción. (b) Use la vida media
de (a) para calcular la constante de velocidad.
✔️ Práctica 14.9.1. Notamos en un ejercicio de práctica anterior que a 25 °C la
descomposición de N2O5(g) en NO2(g) y O2(g)
sigue el primer orden. cinética con k = 3.4 x 10-5 s-1.
¿Cuánto tardará una muestra que originalmente contiene 2.0 atm de N2O5
en alcanzar una presión parcial de 380 torr? (a) 5.7 horas (b) 8.2 horas (c) 11
horas (d) 16 horas (e) 32 horas.
✔️ Práctica 14.9.2. La descomposición de cierto
insecticida en agua a 12 °C sigue una cinética de primer orden con una tasa
constante de 1.45 año-1. Una cantidad de este insecticida se lava en
un lago el 1 de junio, lo que lleva a una concentración de 5.0x10-7
g/cm3. Suponga que la temperatura del lago es constante (de modo que no haya
efectos de variación de temperatura en la velocidad, o que los cambios se
concentración se anulan entre si debido a su naturaleza cíclica). (a) Calcule
t(1/2) para la descomposición del insecticida (b) ¿Cuánto tiempo tarda la
concentración del insecticida en alcanzar la cuarta parte del valor inicial?
✔️ Práctica 14.8.1. Para ciertos productos de reacción A → productos, una gráfica de ln[A]
contra el tiempo produce una línea recta con una pendiente de -3.0 x 10-2
s-1. ¿Cuál de las siguientes afirmaciones es o no es verdadera?: (i)
La reacción sigue una cinética de primer orden. (ii) La constante de velocidad
de la reacción es 3.0 x 10-2 s-1. (iii) La concentración
inicial de [A] era de 1.0 M. (a) Solo una de las afirmaciones es verdadera. (b)
Las afirmaciones (i) y (ii) son verdaderas. (c) Las afirmaciones (i) y (iii)
son verdaderas. (d) Las afirmaciones (ii) y (iii) son verdaderas. (e) Las tres
afirmaciones son verdaderas.
La ecuación (9.3) y relacionadas se puede usar para verificar si una reacción es de primer
orden y para determinar su velocidad constante. Esta ecuación tiene la forma de
la ecuación general para una línea recta, y = mx + b, en la que m es la
pendiente y b es la intersección en y de la línea. Por lo tanto,
para una reacción de primer orden, una gráfica de ln cA
versus tiempo da una línea recta con una pendiente de -k y una
intersección en y de ln cA,0. Una ecuación de primer orden siempre tiene su forma de
logaritmo natural como una línea recta.
La anterior es una prueba importante porque algunos procesos relevantes
para otras áreas del conocimiento se fundamentan en este tipo de matemáticas,
estamos hablando específicamente de los métodos
de datación radiométricos, los cuales deben estandarizarse
inicialmente en laboratorios antes de poderse aplicar a muestras geológicas, y
uno de los pasos de estandarización es precisamente la corroboración de que
estos obedecen a una cinética de primer orden a varias concentraciones
iniciales y finales, lo cual permite construir una curva de interpolación.
En el laboratorio sería imposible determinar todos los puntos de una curva
debido a que muchas cinéticas de reacción son muy demoradas, pero se pueden
hacer mediciones en varios puntos diferentes, y determinar que la tendencia
general es la de la curva predicha por la de la ecuación de Euler. Sin embargo,
la cinética de primer orden no sólo modela a los métodos de datación
radiométricos sino a muchos otros tipos de procesos químicos como por ejemplo la
conversión del metil isonitrilo CH3NC en su isómero acetonitrilo.
Como los experimentos muestran que la reacción es de primer orden, podemos
escribir la ecuación de velocidad:
Llevamos a cabo la reacción a una temperatura a la que el isonitrilo de metilo es un gas de (199 °C) y en la Figura 9‑1a se muestra cómo la presión de este gas varía con el tiempo. Podemos usar la presión como una unidad de concentración para un gas porque sabemos por la ley del gas ideal que la presión es directamente proporcional al número de moles por unidad de volumen. La figura Figura 9‑1b se muestra que una gráfica del logaritmo natural de la presión frente al tiempo es una línea recta. La pendiente de esta línea es -5.1 × 10-5 s-1. (Debe verificar esto usted mismo, recordando que su resultado puede variar ligeramente del nuestro debido a imprecisiones asociadas con la lectura del gráfico). Debido a que la pendiente de la línea es igual a -k, la constante de velocidad para esta reacción es igual a 5.1 × 10-5 s-1.
Figura 9‑1. Datos cinéticos para la conversión de metil isonitrilo en acetonitrilo.
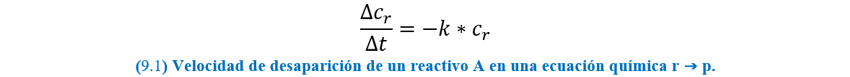









No hay comentarios:
Publicar un comentario