| Ciencias de Joseleg | Química | Química del equillibrio | Cinética química | (Ejercicios) (Introducción) (Generalidades) (Factores que afectan la velocidad de reacción) (Historia) (Velocidad de reacción) (Velocidades de aparición y desaparición) (Relación entre velocidades de aparición, desaparición y reacción) (Ley de velocidad de reacción) (Reacciones de primer orden) (Reacciones de segundo orden) (Reacciones de cero orden) (Vida media) (Energía de activación) (Mecanismo de reacción) (Catalizadores) (Referencias)
Sí se ha
percatado hasta este punto sólo hemos logrado dar instrumentos para calcular
las velocidades de aparición y desaparición, pero no una técnica para calcular
la velocidad de la reacción como un todo, o calcular la velocidad de aparición
o desaparición de una sustancia difícil de medir, en términos de la velocidad
de aparición o desaparición de otra sustancia que sí es fácil de medir, en
otras palabras aparte de esta discusión teórica aún nos falta completar un
algoritmo matemático más robusto.
A
continuación por lo tanto desarrollaremos un modelo matemático para resolver 2
situaciones comunes:
👉 calcular la rapidez de la reacción
como un todo en términos de la rapidez de aparición o desaparición de alguna
sustancia fácil de medir .
👉 calcular la rapidez de aparición o
desaparición de una sustancia difícil de medir “que llamaremos incógnita o
sustancia i”, en términos de la rapidez de aparición o desaparición de una
sustancia fácil de medir “ que llamaremos el dato o sustancia ii”.
Rapidez de la reacción en
términos de la rapidez de aparición o desaparición
Bueno
aunque teóricamente hablamos mucho de la velocidad de la reacción como un todo
(r), experimentalmente a lo que realmente tenemos acceso es a la
velocidad de aparición de un producto o de desaparición de un reactivo (ri),
así que la pregunta evidente es ¿ cómo calcular la velocidad de la reacción
como un todo en términos de la velocidad de aparición o desaparición de un
reactivo? La solución a este dilema es muy sencillo pues simplemente es igualar
la ecuación 5.8, con la ecuación 6.1, con lo que obtenemos la ecuación
7.1. Evidentemente sólo tenemos que cambiar la anotación promedio por la
anotación instantánea para obtener la ecuación 7.2, que será estructuralmente homóloga.
aunque a
primera vista parece una operación algebraicamente evidente nos permite obtener
conclusiones que no son evidentes. la principal conclusión es el hecho de que
si calculamos la rapidez de la reacción completa en términos de un reactivo, obtendremos
que la rapidez del reactivo va en sentido negativo pero su número
estequiométrico también, por lo que la rapidez de una reacción siempre va a ser
un valor positivo, aun cuando empleemos un producto que desaparece con el
tiempo para calcularla.
De lo
anterior también se desprende un aspecto importante de los enunciados de lápiz
y papel, y es que al igual que con el capítulo de entalpía de reacción, es
probable que no nos den los signos correctos para la rapidez de desaparición de
un reactivo, dándonos valores positivos en el enunciado, pero teniendo los que
usar en sentido negativo en las ecuaciones.
Otra
aplicación que no es tan evidente, es el hecho de que la rapidez tasa o
velocidad de la reacción como un todo, es una constante para un momento
infinitesimal de tiempo con respecto a la rapidez tasa o velocidad de aparición o desaparición de las sustancias que involucran a esa reacción química, lo
anterior implica que podemos calcular la rapidez de aparición y desaparición de
una sustancia en términos de la velocidad de aparición o desaparición de otras
sustancia para un momento infinitesimal de tiempo, asumiendo que la rapidez de
la reacción completa es la constante que las vincula.
La velocidad de aparición
en términos de la velocidad de desaparición
En
ocasiones es posible que necesitemos calcular la velocidad de una sustancia en
términos de la velocidad de reacción de otra sustancia.
🟦 DEMOSTRACION: Hallar la ecuación de velocidad de
aparición/desaparición de una sustancia en términos de la
aparición/desaparición de otra sustancia y los cambios de concentraciones de esa sustancias.
Y evidentemente la ecuación anterior se puede
extender para las relaciones instantáneas.
Con lo cual vuelve a aparecer un cociente que hemos venido estudiando desde
el capítulo de estequiometría y es el radio estequiométrico (vi/vd),
el cual a su vez requiere que la ecuación química que modela la situación esté
balanceada para masa y carga.
Química de Chang 10
✔️ (Ejemplo 13.2): Considere la reacción 4NO2(g)
+ O2(g) → 2N2O5(g) Suponga que, en un momento
particular durante la reacción, el oxígeno molecular está reaccionando a una
velocidad de 0.024 M/s. (a) ¿A qué velocidad se forma N2O5?
(b) ¿A qué velocidad reacciona el NO2?
✔️ (Práctica 13.2): Considere la reacción 4PH3(g)
→ P4(g) + 6H2(g) Suponga que, en un momento particular
durante la reacción, se forma hidrógeno molecular a una velocidad de 0.078 M/s.
(a) ¿A qué velocidad se está formando P4? (b) ¿A qué velocidad está
reaccionando PH3?
✔️ (Problema 13.7): Considere la reacción 2NO(g) + O2(g)
→ 2NO2(g) Suponga que en un momento particular durante la reacción
el óxido nítrico (NO) reacciona a una velocidad de 0.066 M/s. a) ¿A qué
velocidad se forma NO2? (b) ¿A qué velocidad reacciona el oxígeno
molecular?
✔️ (Problema 13.8): Considere la reacción N2(g) + 3H2(g) → 2NH3(g)
Suponga que en un momento particular durante la reacción, el hidrógeno molecular
reacciona a una velocidad de 0.074 M/s. (a) ¿A qué velocidad se forma amoníaco?
(b) ¿A qué velocidad reacciona el nitrógeno molecular?
Química la ciencia central13
✔️ (Práctica 14.1 i) En un frasco de exactamente un
litro de volumen se tiene el gas a como reactivo inicialmente con una cantidad
de sustancia de 1.00 mol, a los 20 segundos es de 0.54 mol, a los 40 segundos
es de 0.30 mol, y a los 60 segundos es de 0.16 mol. Confirmar que hay 0.84 mol
de B a los 60 segundos. La ecuación química de la reacción es A → B
✔️ (Práctica 14.1.2) En un frasco de exactamente un
litro de volumen se tiene el gas a como reactivo inicialmente con una cantidad
de sustancia de 1.00 mol, a los 20 segundos es de 0.54 mol, a los 40 segundos
es de 0.30 mol, y a los 60 segundos es de 0.16 mol. Calcular la tasa promedio
de aparición de B durante el intervalo de tiempo de 0 s a 40 s.
✔️ (Problema 14.19a) Considere la siguiente reacción
acuosa hipotética: A → B. Un matraz se carga con 0.065 mol de A en un volumen
total de 100.0 mL. Se recopilan los siguientes datos: en 0 minutos 0.065 mol,
en 10 minutos 0.051 mol, en 20 minutos 0.042 mol, en 30 minutos 0.036 mol en 40
minutos 0.031 mol. Calcule el número de moles de B en cada momento de la tabla,
suponiendo que no hay moléculas de B en el momento cero, y que A se convierte
limpiamente en B sin intermediarios.
✔️ (Problema 14.19c) Considere la siguiente reacción acuosa hipotética: A → B. Un matraz se
carga con 0.065 mol de A en un volumen total de 100.0 mL. Se recopilan los
siguientes datos: en 0 minutos 0.065 mol, en 10 minutos 0.051 mol, en 20 minutos
0.042 mol, en 30 minutos 0.036 mol en 40 minutos 0.031 mol. Entre t = 10 min y
t = 30 min, ¿cuál es la tasa promedio de aparición de B en unidades de M/s?
Suponga que el volumen de la solución es constante.
✔️ (Problema 14.20) Un matraz se carga con 0.100 mol de A y se deja reaccionar para formar B de acuerdo con la reacción hipotética en fase gaseosa A(g)→ B(g). Se recogen los siguientes datos: (a) Calcule el número de moles de B en cada momento de la tabla, suponiendo que A se convierte limpiamente en B sin intermediarios. (b) Calcule la tasa promedio de desaparición de A para cada intervalo de 40 s en unidades de mol/s. (c) ¿Cuál de los siguientes sería necesario para calcular la velocidad en unidades de concentración por tiempo: (i) la presión del gas en cada momento, (ii) el volumen del matraz de reacción, (iii) la temperatura, o (iv) el peso molecular de A?
Efecto de la ley de la conservación de la masa
Por definición sabemos que la ley de la
conservación de la masa debe aplicarse, en ese contexto queremos decir que la
masa de reacción en todo momento es constante aunque las partículas en su
interior estén cambiando, lo cual se puede traducir como:
Todo parámetro vinculado a la masa también
tendrá una vinculación a la ley de la conservación de la masa, pero no
exactamente igual. Lo que si asumiremos es que:
Para poder evaluar cual es el efecto de la conservación de la masa en el número de partículas, lo que haremos es tomar una tabla de cinética de concentración contra tiempo de varias sustancias, vinculadas por una reacción química cuyos números estequiométricos sean diferentes de uno, como esta:
Tabla 7‑1. Cambios de
concentraciones de reactivos y productos en la reacción química 2NO+O2→2NO2. Si siente que los intervalos de tiempo son un poco arbitrarios, es
porque la razón de estos es que son intervalos en los cuales las diferencias de
concentraciones son iguales.
Ahora analíticamente lo que haremos
es:
🟦 DEMOSTRACION: Hallar una ecuación que permita calcular
la diferencia de cantidad de sustancia total, y la cantidad de sustancia total,
en términos de los valores equivalentes de una sola sustancia medida.
Con lo cual obtenemos la forma general:
Tenga en cuenta que para calcular la cantidad
instantánea en lugar de la diferencia de cantidades totales, el intervalo de
tiempo entre la diferencia total y la diferencia de la sustancia dato debe ser
el mismo.
Ejemplo
✔️ (Ejemplo) Se sabe que en el intervalo desde cero a 285 segundos la concentración
molar de NO paso de 0.010 a 0.009 mol, de O2 paso de 0.010 a 0.0095 mol y de
NO2 paso de 0.000 a 0.001 mol. Calcular los moles totales en 285 segundos con
(a) toda la serie de datos a 285 segundos y (b) solo con los datos de NO y la
ecuación química balanceada 2 NO + O2 → 2 NO2.
Rapidez
de la reacción en términos de las variables de gas
En ocasiones resulta más práctico en ecuaciones de producción o de
absorción de gases medir parámetros como la presión o el volumen, con los
cuales podemos llegar a la cantidad de sustancia, por lo que la definición de
rapidez de reacción puede expresarse para parámetros diferentes de masa,
cantidad de sustancia y concentración líquida.
🟦 DEMOSTRACION: Hallar la función que permite calcular la rapidez de una reacción en
términos de la presión a volumen y temperatura constante.



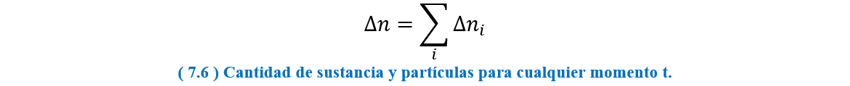





No hay comentarios:
Publicar un comentario