Equilibrio químico: 13. Energía de activación | ⏩ Cinética química

| Ciencias de Joseleg | Química | Química del equillibrio | Cinética química | (Ejercicios) (Introducción) (Generalidades) (Factores que afectan la velocidad de reacción) (Historia) (Velocidad de reacción) (Velocidades de aparición y desaparición) (Relación entre velocidades de aparición, desaparición y reacción) (Ley de velocidad de reacción) (Reacciones de primer orden) (Reacciones de segundo orden) (Reacciones de cero orden) (Vida media) (Energía de activación) (Mecanismo de reacción) (Catalizadores) (Referencias)

Las velocidades de reacción de la mayoría de las reacciones químicas aumentan a medida que aumenta la temperatura. Por ejemplo, la masa aumenta más rápido a temperatura ambiente que cuando está refrigerada, y las plantas crecen más rápidamente en clima cálido que en frío. Podemos ver el efecto de la temperatura sobre la velocidad de reacción al observar una reacción de quimioluminiscencia (una que produce luz), como la de las barras de luz Cyalume® (Figura 13‑1.).

Figura 13‑1. La temperatura afecta la velocidad de la reacción de quimioluminiscencia en barras de luz: la reacción de quimioluminiscencia ocurre más rápidamente en agua caliente y se produce más luz.

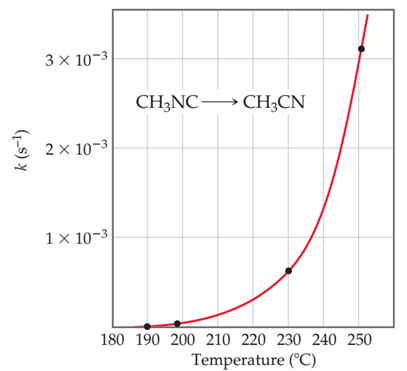
¿Cómo se refleja este efecto de temperatura observado experimentalmente en la ley de velocidad de reacción? La velocidad más rápida a una temperatura más alta se debe a un aumento en la velocidad constante al aumentar la temperatura. Por ejemplo, reconsideremos la reacción de primer orden que vimos en la Figura 12‑1, a saber, CH₃NC →CH3CN.

Figura 13‑2. Dependencia de la temperatura de la constante de velocidad para la conversión de metilisonitrilo en acetonitrilo.

La Figura 13‑2 muestra la constante de velocidad para esta reacción en función de la temperatura. La velocidad constante y, por lo tanto, la velocidad de la reacción aumenta rápidamente con la temperatura, aproximadamente el doble por cada aumento de 10 °C.

Modelo de colisiones

Las velocidades de reacción se ven afectadas tanto por las concentraciones de reactivos como por la temperatura. El modelo de colisión, basado en la teoría cinético-molecular (química de gases), explica ambos efectos a nivel molecular. La idea central del modelo de colisión es que las moléculas deben colisionar para reaccionar. Cuanto mayor es el número de colisiones por segundo, mayor es la velocidad de reacción. A medida que aumenta la concentración de reactivo, por lo tanto, aumenta el número de colisiones, lo que conduce a un aumento en la velocidad de reacción. De acuerdo con la teoría cinética molecular de los gases, el aumento de la temperatura aumenta las velocidades moleculares. A medida que las moléculas se mueven más rápido, chocan con más fuerza (con más energía) y con mayor frecuencia, aumentando las velocidades de reacción.

Para que ocurra una reacción, sin embargo, se requiere más que simplemente una colisión: debe ser el tipo correcto de colisión. Para la mayoría de las reacciones, de hecho, solo una pequeña fracción de colisiones conduce a una reacción. Por ejemplo, en una mezcla de H₂ e I₂ a temperaturas y presiones normales, cada molécula sufre aproximadamente 10¹⁰ colisiones por segundo. Si cada colisión entre H₂ e I₂ resultara en la formación de HI, la reacción terminaría en mucho menos de un segundo. En cambio, a temperatura ambiente, la reacción avanza muy lentamente porque solo una de cada 10¹³ colisiones produce una reacción. ¿Qué impide que la reacción ocurra más rápidamente?

Orientación de la molécula

En la mayoría de las reacciones, las colisiones entre moléculas provocan una reacción química solo si las moléculas están orientadas de cierta manera cuando colisionan.

Figura 13‑3. Las colisiones moleculares pueden o no conducir a una reacción química entre Cl y NOCl.

Las orientaciones relativas de las moléculas durante la colisión determinan si los átomos están posicionados adecuadamente para formar nuevos enlaces. Por ejemplo, considere la reacción Cl + NOCl→ NO + Cl₂., que tiene lugar si la colisión une a los átomos de Cl para formar Cl₂, como se muestra en el panel superior de la Figura 13‑3. En contraste, en la colisión que se muestra en el panel inferior, los dos átomos de Cl no chocan directamente entre sí, y no se forman productos.

Energía de activación

La orientación molecular no es el único factor que influye en si una colisión molecular producirá una reacción. En 1888, el químico sueco Svante Arrhenius sugirió que las moléculas deben poseer una cierta cantidad mínima de energía para reaccionar. Según el modelo de colisión, esta energía proviene de las energías cinéticas de las moléculas en colisión. Tras la colisión, la energía cinética de las moléculas se puede utilizar para estirar, doblar y finalmente romper enlaces, lo que lleva a reacciones químicas. Es decir, la energía cinética se usa para cambiar la energía potencial de la molécula. Si las moléculas se mueven muy lentamente, en otras palabras, con muy poca energía cinética, simplemente rebotan entre sí sin cambiar. La energía mínima requerida para iniciar una reacción química se llama energía de activación, E_a, y su valor varía de una reacción a otra.

Figura 13‑4. Se necesita energía para superar una barrera entre los estados inicial y final.

La situación durante las reacciones es análoga a la que se muestra en la Figura 13‑4. El golfista golpea la pelota para que se mueva sobre la colina en dirección a la copa. La colina es una barrera entre la pelota y la copa. Para alcanzar la copa, el jugador debe impartir suficiente energía cinética con el putter para mover la pelota hacia la parte superior de la barrera. Si no imparte suficiente energía, la pelota rodará hasta la mitad de la colina y luego regresará hacia él. Del mismo modo, las moléculas requieren una cierta energía mínima para romper los enlaces existentes durante una reacción química. Podemos pensar en esta energía mínima como una barrera energética. En el reordenamiento de metil isonitrilo a acetonitrilo, por ejemplo, podríamos imaginar la reacción pasando a través de un estado intermedio en el que la porción N C de la molécula de metil isonitrilo está de lado.

La Figura 13‑5 muestra que se debe suministrar energía para estirar el enlace entre el grupo H₃C y el grupo N ‚C para permitir que el grupo N C gire. Después de que el grupo N C se ha torcido lo suficiente, el enlace C C comienza a formarse y la energía de la molécula cae.

Figura 13‑5. Perfil energético para la conversión de metil isonitrilo H3CNC en su isómero acetonitrilo H₃CCN.

Por lo tanto, la barrera para la formación de acetonitrilo representa la energía necesaria para forzar a la molécula a pasar por un estado intermedio relativamente inestable, análogo a forzar la bola en la Figura 13‑4 sobre la colina. La diferencia entre la energía de la molécula inicial y la energía más alta a lo largo de la vía de reacción es la energía de activación, E_a. La molécula que tiene la disposición de los átomos que se muestra en la parte superior de la barrera se denomina complejo activado o estado de transición.

La conversión de H₃C N≡C a H₃C C≡N es exotérmica. Por lo tanto, la Figura 13‑5 muestra que el producto tiene una energía menor que el reactivo. Sin embargo, el cambio de energía para la reacción, ∆E, no tiene efecto sobre la velocidad de reacción. La tasa depende de la magnitud de E_a; en general:

cuanto menor es el valor de E_a, más rápida es la reacción.

Tenga en cuenta que la reacción inversa es endotérmica. La energía de activación para la reacción inversa es igual a la energía que debe superarse si se acerca a la barrera desde la derecha: ∆E+E_a. Por lo tanto, alcanzar el complejo activado para la reacción inversa requiere más energía que para la reacción directa; para esta reacción, hay una barrera más grande que vencer de derecha a izquierda que de izquierda a derecha.

Brown13 química la ciencia central

✔ muestra 14.10. Ordenar las reacciones modeladas con los siguientes perfiles de energía de activación, desde la mas lenta a la mas rápida.

Cualquier molécula particular de metil isonitrilo adquiere energía suficiente para superar la barrera de energía a través de colisiones con otras moléculas. Recordemos de la teoría cinética-molecular de los gases que, en cualquier instante, las moléculas de gas se distribuyen en energía en un amplio rango. La Figura 13‑6 muestra la distribución de energías cinéticas para dos temperaturas, comparándolas con la energía mínima necesaria para la reacción, E_a. A la temperatura más alta, una fracción mucho mayor de las moléculas tiene una energía cinética mayor que E_a, lo que conduce a una mayor velocidad de reacción.

Figura 13‑6. El efecto de la temperatura sobre la distribución de las energías cinéticas de las moléculas en una muestra.

Para una colección de moléculas en la fase gaseosa, la fracción de moléculas que tienen energía cinética igual o mayor que viene dada por la expresión:

En esta ecuación, R es la constante de los gases ideales (8.14 J/mol-K) y T es la temperatura absoluta. Para tener una idea de la magnitud de f, supongamos que E_a es 100 kJ/mol, un valor típico de muchas reacciones, y que T es 300 K. El valor calculado de f es 3.9×10^-18, un número extremadamente pequeño. A 320 K, f= 4.7×10^-17. Por lo tanto, solo un aumento de 20° en la temperatura produce un aumento de más de diez veces en la fracción de moléculas que poseen al menos 100 kJ/mol de energía.

La ecuación de Arrhenius

Arrhenius señaló que, para la mayoría de las reacciones, el aumento de la velocidad con el aumento de la temperatura no es lineal (Figura 13‑2). Encontró que la mayoría de los datos de velocidad de reacción obedecían a una ecuación basada en:

👉 la fracción de moléculas que poseen energía E_a o mayor,

👉 el número de colisiones por segundo, y

👉 la fracción de colisiones que tienen la orientación apropiada. Estos tres factores se incorporan a la ecuación de Arrhenius:

El factor de frecuencia, A, es constante, o casi, a medida que varía la temperatura. Este factor está relacionado con la frecuencia de las colisiones y la probabilidad de que las colisiones estén orientadas favorablemente para la reacción, debido a que la frecuencia de colisión aumenta con la temperatura, A también tiene cierta dependencia de la temperatura, pero esta dependencia es mucho menor que el término exponencial. Por lo tanto, A se considera aproximadamente constante. A medida que aumenta la magnitud de E_a,k disminuye porque la fracción de moléculas que poseen la energía requerida es menor. Por lo tanto, a valores fijos de T y A, las velocidades de reacción disminuyen a medida que E_a aumenta.

Usando la ecuación de Arrhenius

🟦 DEMOSTRACIÓN. Modificar la ecuación de Arrhenius de energía de activación para hallar: su forma lineal con logaritmos naturales, su primer forma dinámica que permite calcular la energía de activación a partir de una serie de datos de k vs T, y su segunda forma dinámica que permite calcular k en términos de k₀ y la energía de activación.

Opción gráfica

La ecuación 13.5 muestra una opción gráfica para calcular la energía de activación. Una gráfica de ln k versus 1/T es una línea con una pendiente igual a –E_a/R y una intersección en (y) igual a ln A. Por lo tanto, la energía de activación se puede determinar midiendo k en una serie de temperaturas, graficando ln k versus 1/T, y calculando E_a a partir de la pendiente de la línea resultante. Adicionalmente, en la opción gráfica vamos a tener dos subopciones para resolver esto:

👉 Opción manual: deberemos elegir: de la línea recta de manera arbitraria y calcular la pendiente manualmente. esta opción tiene el problema de que, si los datos no apoyan una línea recta perfecta, podremos calcular una energía de activación errónea, si elegimos precisamente aquellos puntos que más se desvían de la línea recta. De allí que para esta estrategia usted debe analizar la gráfica y escoger los puntos que más se aproximen a la recta.

👉 Opción automática: básicamente se trata de usar Excel, mediante los comandos insertar → Gráficos → Dispersión → Dispersión con líneas suavizadas y marcadores → seleccionar la recta en la gráfica → clic derecho → insertar línea de tendencia → lineal y activar los comandos de ecuación del gráfico y valor de Rcuadrado. Al graficar en Excel tenga cuidado de colocar primero la columna para el eje (x), y luego la columna para el eje (y) en la tabla de datos antes que insertar una gráfica de dispersión.

Opción analítica

La ecuación 13.4 nos muestra una opción analítica para calcular la energía de activación. Debido a que podemos usar una variedad de parejas de datos, lo aconsejable es calcular para las parejas adyacentes presentes y luego calcular el promedio aritmético.

El valor de la constante de los gases ideales

Recuerde que la constante de gases ideales deberá expresarse en unidades de energía: 8.314 J /mol-K. Si lo que desea es expresar directo en kilojulios debe usar 8.314 x 10^-3 kJ /mol-K.

Cual opción es más conveniente

Aunque la teoría nos dice que la gráfica ln k vs 1/T debe ser una línea recta, en la práctica los datos pueden no tener una relación de línea recta simplemente debido a errores de muestreo, errores experimentales entre otros, por lo que el método gráfico establecido por el libro de texto como la química de Chang presenta un problema, elegir arbitrariamente las coordenadas para dibujar la línea recta nos puede llevar a generar valores de energía de activación diferentes aún dentro de la misma serie de datos, incluso los valores que obtengamos como resultado de una regresión lineal o del promedio de las energías de activación para cada pareja posible en la serie de datos puede llevarnos a resultados que no son exactamente iguales. La pregunta es ¿cuándo esperar que los valores por las dos rutas sean diferentes? y la respuesta radica en el valor R² de la regresión lineal que nos da Excel:

👉 para un valor de R² igual a 1 significa que la regresión lineal se ajusta perfectamente a un modelo de línea recta, y en consecuencia es de esperarse que la energía de activación calculada gráficamente y analíticamente sean iguales.

👉 si el valor de R² de la regresión lineal en Excel es menor que uno, deberemos esperar que las energías de activación calculadas por la ruta gráfica y por la ruta analítica tengan sus diferencias. las diferencias aumentarán a medida que el valor de R² se haga más diferente de 1.

Química de Chang10

✔ Ejemplo 13.8. Las constantes de velocidad para la descomposición del acetaldehído CH₃CHO(g) → CH₄(g) + CO(g) se midieron a cinco temperaturas diferentes. Los datos se muestran en la tabla. Grafique ln k versus 1/T y determine la energía de activación (en kJ/mol) para la reacción. Tenga en cuenta que la reacción es de orden "3/2" en CH₃CHO, por lo que k tiene las unidades de 1/M^1/2-s.

✔ Práctica 13.8. La constante de velocidad de segundo orden para la descomposición del óxido nitroso (N₂O) en una molécula de nitrógeno y un átomo de oxígeno se ha medido a diferentes temperaturas, y esta dada en la tabla de datos adjunta. Determine gráficamente la energía de activación de la reacción.

✔ Ejemplo 13.9. La constante de velocidad de una reacción de primer orden es 3.46 × 10^-2 s^-1 a 298 K. ¿Cuál es la constante de velocidad a 350 K si la energía de activación de la reacción es de 50.2 kJ/mol?

✔ Práctica 13.9. La constante de velocidad de primer orden para la reacción de cloruro de metilo (CH₃Cl) con agua para producir metanol (CH₃OH) y ácido clorhídrico (HCl) es 3.32 x 10^-10 s^-1 a 25°C. Calcule la constante de velocidad a 40 °C si la energía de activación es de 116 kJ/mol.

Brown13 química la ciencia central

✔ muestra 14.11a. La siguiente tabla muestra las constantes de velocidad para el reordenamiento del metilisonitrilo a varias temperaturas: A partir de estos datos, calcule la energía de activación para la reacción.

✔ muestra 14.11b. La siguiente tabla muestra las constantes de velocidad para el reordenamiento del metilisonitrilo a varias temperaturas: ¿Cuál es el valor de la constante de velocidad a 430.0 K?

✔ Práctica 14.11.1. La siguiente tabla muestra las constantes de velocidad para el reordenamiento del metilisonitrilo a varias temperaturas. Tenga en cuenta que la energía de activación fue de 1.60 x 10² kJ/mol. ¿cuál de las siguientes es la constante de velocidad para el reordenamiento del metilisonitrilo a 320 °C? (a) 8.1 x 10^-15s^-1 (b) 2.2 x 10^-13 s^-1 (c) 2.7 x 10^-9 s^-1 (d) 2.3 x 10^-1 s^-1 (e) 9.2 x 10³ s^-1.