| Ciencias de Joseleg
| Química | Química del equillibrio | Cinética
química | (Ejercicios) (Introducción)
(Generalidades)
(Factores
que afectan la velocidad de reacción) (Historia)
(Velocidad
de reacción) (Velocidades
de aparición y desaparición) (Relación
entre velocidades de aparición, desaparición y reacción) (Ley
de velocidad de reacción) (Reacciones
de primer orden) (Reacciones
de segundo orden) (Reacciones
de cero orden) (Vida
media) (Energía
de activación) (Mecanismo
de reacción) (Catalizadores)
(Referencias)
Una vez
que hemos logrado unificar una sola definición para la rapidez promedio de la
reacción, ahora debemos proponer las velocidades de aparición de producto y
desaparición de reactivo que simbolizaremos usando el símbolo de rapidez de
reacción y los símbolos de las sustancias respectivas como subíndices: rr
= rapidez de desaparición del reactivo; rp = rapidez de aparición
del producto. Si no
conocemos si la sustancia es un reactivo o un producto, es decir para proponer
la forma más general de la ecuación, usaremos el subíndice (i).
Negativos y positivos
Por definición si calculamos la rapidez de reacción para un reactivo, nos
daremos cuenta que la concentración final es menor que la concentración inicial,
de allí que la rapidez de la reacción de un reactivo es negativa, y una
pendiente negativa implica una recta descendente, o una curva descendente en
caso de que tengamos muchos valores diferentes de rapidez promedio.
el problema es que por convención, cuando expresamos los valores del rap de
desaparición para la solución de muchos ejercicios de lápiz y papel, ofrecemos
valores de solución positivos, puesto que estamos calculando el negativo de la
rapidez de desaparición -r(reactivo), de manera implícita, lo cual puede llegar
a causar confusiones cuando tratamos de relacionar la rapidez de la reacción
que aparece en una gráfica o experimento “que nuevamente por definición del
cálculo es una pendiente con signo negativo porque desciende”, en contraste con
la rapidez de desaparición que ofrecemos en las soluciones de los ejercicios de
lápiz y papel, que por convención son valores positivos.
dado que la vasta mayoría de libros de texto realiza esta incongruencia, no
la podremos corregir en este curso de química general, simplemente la vamos a
advertir. y cuando nos toque calcular la rapidez de la desaparición de un
reactivo, y sepamos de antemano que tengo que dar una solución positiva porque
así lo dicta el solucionario un libro de texto, expondré el parámetro de
rapidez como un valor negativo -r(reactivo).
Rectas y curvas
A pesar de los nombres pomposos que podamos darle a la ecuación 5.8 en su
aplicación en el contexto de la cinética química, desde la perspectiva
matemática es una pendiente de recta, el problema es que experimentalmente, la
rapidez de la reacción no es constante y no manifiesta rectas, cómo lo
expondremos en los siguientes ejemplos:
En soluciones acuosas, el
bromo molecular reacciona con el ácido fórmico (HCOOH) de la siguiente manera:
Br2(aq) + HCOOH(aq) → 2Br-(aq) + 2H+(aq) +
CO2(g). El bromo molecular Br2 es de color marrón rojizo. Todas las
demás especies en la reacción son incoloras. A medida que avanza la reacción,
la concentración de Br2 disminuye constantemente y su color se
desvanece.
Figura 6‑1. De izquierda a derecha: La disminución de la
concentración de bromo a medida que transcurre el tiempo se manifiesta como una
pérdida de color (de izquierda a derecha).
Esta pérdida de color y, por
lo tanto, de concentración se puede monitorear fácilmente con un espectrómetro,
que registra la cantidad de luz visible absorbida por el bromo. Ahora ya dependiendo
de qué tan tecnológico o sea tu espectrómetro, podrás tomar medidas discretas (sólo
algunas medidas a lo largo del tiempo de reacción), o medidas más continuas (una
mayor cantidad de datos a lo largo del tiempo de reacción).
✔️ ejemplo: En una determinada reacción química consume bromo elemental disuelto en
agua, la concentración de bromo se determinó por medio de espectrometría para
intervalos de tiempo arbitrarios. Al iniciar la reacción la concentración de
bromo era de 0.01200 M, a los 50 segundos era de 0.01010 M, y a los 100
segundos era de 0.00864 M. Calcule la velocidad promedio a la que el bromo
desaparece en los intervalos de cero a 50 segundos, y compararla con el
intervalo de 50 a 100 segundos.
Química la
ciencia central 13
✔️ (Práctica 14.1.2) En un frasco de exactamente un litro de volumen se tiene el gas a como
reactivo inicialmente con una cantidad de sustancia de 1.00 mol, a los 20 segundos
es de 0.54 mol, a los 40 segundos es de 0.30 mol, y a los 60 segundos es de
0.16 mol. Confirmar que la velocidad de desaparición de A en el intervalo de 0
a 20 segundos es mayor que en el intervalo de 40 a 60 segundos.
✔️ (Problema 14.19b) Considere la siguiente reacción acuosa hipotética: A → B. Un matraz se
carga con 0.065 mol de A en un volumen total de 100.0 mL. Se recopilan los
siguientes datos: en 0 segundos 0.065 mol, en 10 segundos 0.051 mol, en 20
segundos 0.042 mol, en 30 segundos 0.036 mol en 40 segundos 0.031 mol. Calcule
la tasa promedio de desaparición de A para cada intervalo de 10 min en unidades
de M/s.
Estos
cálculos demuestran que la velocidad promedio de la reacción depende del
intervalo de tiempo que elijamosm en otras palabras, la rapidez de la reacción
no es constante. Para recalcar este punto ahora consideremos la reacción entre
el cloruro de butilo C4H9Cl y el agua para formar alcohol
butílico C4H9OH y ácido clorhídrico:
Supongamos que preparamos una solución acuosa de C4H9Cl
0.1000 M y luego medimos la concentración de C4H9Cl en
varios momentos después del tiempo cero (que es el instante en que se mezclan
los reactivos, iniciando así la reacción). Podemos usar los datos resultantes,
que se muestran en las dos primeras columnas de la tabla 6.1, para calcular la
tasa promedio de desaparición de C4H9Cl durante varios
intervalos de tiempo; Estas tasas se dan en la tercera columna.
Tabla 6‑1. Datos de velocidad para la
reacción de C4H9Cl con agua
Observe que la tasa promedio disminuye
durante cada intervalo de 50 s para las primeras mediciones y continúa
disminuyendo en intervalos aún mayores a través de las mediciones restantes. Es
típico que las velocidades disminuyan a medida que avanza la reacción porque
disminuye la concentración de reactivos.
Visualizando la rapidez de
aparición y desaparición
El hecho de que las tasas de aparición de producto y desaparición de reactivo no sean constantes, implica necesariamente que cuando grafiquemos en el plano cartesiano concentración contra tiempo, obtendremos curvas en lugar de rectas. Consideremos la reacción hipotética A→B, representada en la siguiente figura.
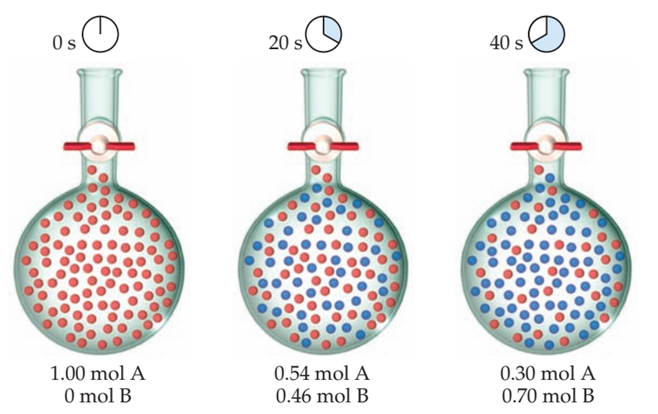
Figura 6‑2. Progreso de una reacción
hipotética A→B. El volumen del matraz es 1.0 L.
Cada esfera roja representa 0.01 mol de A, cada esfera azul representa 0.01
mol de B, y el recipiente tiene un volumen de 1.00 L. Al comienzo de la
reacción, hay 1.00 mol A, entonces la concentración es 1.00 mol/L = 1.00 M.
Después de 20 s, la concentración de A ha caído a 0.54 M y la concentración de
B ha aumentado a 0.46 M. La suma de las concentraciones todavía es 1.00 M porque
se produce 1 mol de B por cada mol de A que reacciona. Después de 40 s, la
concentración de A es de 0.30 M y la de B es de 0.70 M.
Figura 6‑3. Gráfica de las velocidades de aparición y desaparición
de productos y reactivos en unidades de moléculas/segundos. Tenga en cuenta que las únicas medidas reales son los
puntos, por lo que estamos trabajando con cálculos de estado o promedios, en
lugar de cálculos infinitesimales o instantáneos.
Empleando
las herramientas que hemos aprendido en el curso de cálculo nos podemos dar
cuenta que, a medida que el tiempo tiende a infinito, la rapidez de aparición
de producto y desaparición de reactivo tenderá a cero. Ese análisis matemático
le podemos dar un sentido químico en el hecho de que, a medida que el tiempo
tiene infinito, la cantidad de partículas de reactivos se hacen más escasas y
por lo tanto más improbable que se encuentren para reaccionar y producir las
respectivas partículas de producto, de allí que la cantidad de eventos de
reacción por unidad de tiempo va disminuyendo paulatinamente.
Rapidez de aparición y
desaparición instantánea
Otro aspecto del cálculo que debemos notar de la figura 6-3, es el hecho de que los puntos realmente medidos se encuentran separados por una cantidad de tiempo sensible, de allí que esta medición sólo nos permite aproximarnos a una velocidad de reacción promedio. A medida que tomemos más medidas en una menor cantidad de tiempo podremos obtener una gráfica más continua, y por ende aproximarnos a la velocidad de reacción instantánea.
Figura 6‑4. Tasa de cambio instantánea de
masa de oxígeno contra tiempo en un contenedor de 1 L para la reacción 2C2H5(g)
→ 4 NO2(g) + O2(g). La pendiente instantánea de esta
curva se define como la tasa de formación de O2 con respecto al tiempo, dado
que es una curva, debemos emplear técnicas del cálculo infinitesimal para
determinar la tasa de cambio instantánea.
La tasa de cambio instantánea δci/δti es
el valor para la tasa de cambio en un intervalo de tiempo muy pequeño e
idealmente infinitesimal.
El problema con la gráfica de concentración por unidad de tiempo es que
¡tenemos una curva! ¿Cuál es el problema con que sea curva? El problema con una
gráfica curva es que los valores para la tasa de cambio instantánea son
diferentes de la obtenida para la tasa de cambio promedio, en otras palabras,
no podemos usar pendientes de líneas rectas para determinar la tasa de cambio
instantánea, ya que esta formación es una curva.
Métodos experimentales
Para aproximarse experimentalmente una tasa de reacción instantánea δci/δti
hay que tener en cuenta las limitaciones experimentales y que tipo de tasa de
reacción.
Con limitaciones experimentales nos referimos a que la cantidad de medidas
de concentración que podemos realizar por unidad de tiempo con nuestro
instrumento de laboratorio, en otras palabras, si contamos con instrumentos
experimentales más sofisticados es probable que logremos obtener una mayor
cantidad de medición en una menor cantidad de tiempo.
con respecto al tipo de reacción hacemos referencia a que algunas
reacciones son lo suficientemente lentas como para permitir una toma de datos
relativamente continua con instrumentos no muy sofisticados.
Los métodos químicos para determinar la cantidad de sustancia producida y
consumida por lo general permiten evaluar una cantidad limitada de puntos, lo
cual genera una serie de tasas de reacción promedio que unen los puntos
determinados. Los métodos físicos por el contrario permiten la determinación
continua de las cantidades de sustancia producida o consumida durante el
intervalo de tiempo analizado. Debido a que las cantidades de producto y
reactivo están relacionadas de manera estequiométrica, cualquier especie
química dentro de la reacción puede ser empleada para expresar la tasa de
cambio de la reacción y de las demás sustancias como veremos más adelante.
Figura 6‑5. Tasas de reacción en una
determinación discontinua.
Sí se ha
percatado hasta este punto sólo hemos logrado dar instrumentos para calcular
las velocidades de aparición y desaparición, pero no una técnica para calcular
la velocidad de la reacción como un todo, o calcular la velocidad de aparición
o desaparición de una sustancia difícil de medir, en términos de la velocidad
de aparición o desaparición de otra sustancia que sí es fácil de medir, en
otras palabras aparte de esta discusión teórica aún nos falta completar un
algoritmo matemático más robusto.
En caso de que no contemos con los instrumentos necesarios para hallar la
verdadera velocidad instantánea a través de la función derivada, podemos
obtener una aproximación a la velocidad instantánea empleando la pendiente de
un punto en el tiempo, que es De hecho la ruta que nos aconsejan los libros de
texto de química general.
Figura 6‑6. Concentración de cloruro de
butilo C4H9Cl en función del tiempo.
La gráfica
anterior implica que los libros de texto nos piden hallar velocidades
instantáneas con la fórmula de la velocidad promedio, y descaradamente así lo
indican. relieve hecho
los libros de texto de química general solo introducen técnicas sofisticadas de
cálculo cuando introducimos los conceptos de orden de reacción. Dado lo
anterior, en ejercicios de lápiz y papel donde
nos piden hallar la rapidez de reacción instantánea, en realidad nos estarán
pidiendo calcular la rapidez de la reacción promedio para un punto determinado.
Química la ciencia central 13
✔️ (Problema 14.21d) Se estudió la isomerización del
metilisonitrilo CH3NC a acetonitrilo CH3CN en fase
gaseosa a 215 °C, y se obtuvieron los siguientes datos: 0 s 0.01650 M de CH3NC;
2000 s 0.01100 M de CH3NC; 5000 s 0.00591 M de CH3NC;
8000 s 0.00314 M de CH3NC; 12000 s 0.00137 M de CH3NC;
15000 s 0.00074 M de CH3NC. (d) Grafique la concentración molar de
CH3NC contra el tiempo y determine las tasas instantáneas en M/s en
t = 5000 s y t = 8000s.
✔️ (Problema 14.22d) Se midió la velocidad de
desaparición de HCl para la siguiente reacción: CH3OH + HCl → CH3Cl + H2O. Se
recogieron los siguientes datos: a 0.0 min 1.85 molar, a 54.0 minutos 1.58
molar. a 107.0 minutos 1.36 molar, a 215.0 minutos 1.02 molar, a 430.0 minutos
0.580 molar. (d) Grafique [HCl] contra el tiempo y determine las velocidades
instantáneas en M/min y M/s en t = 75.0 min y t = 250 min.











No hay comentarios:
Publicar un comentario